
About the Nickel Model Library
The Nickel Model Library is a package of property models used to set up calculations in the Property Model Calculator. The library includes five models intended for those working in the nickel industry: Antiphase Boundary Energy, Coarsening, Equilibrium with Freeze-in Temperature, Solvus for Ordered Phase, and Strain-Age Cracking.
The Nickel Model Library is available for free to all users who have licenses for the nickel databases TCNI (version 11 or newer) and MOBNI (version 5 or newer) and valid Maintenance & Support Subscription (M&SS).
Antiphase Boundary Energy Model
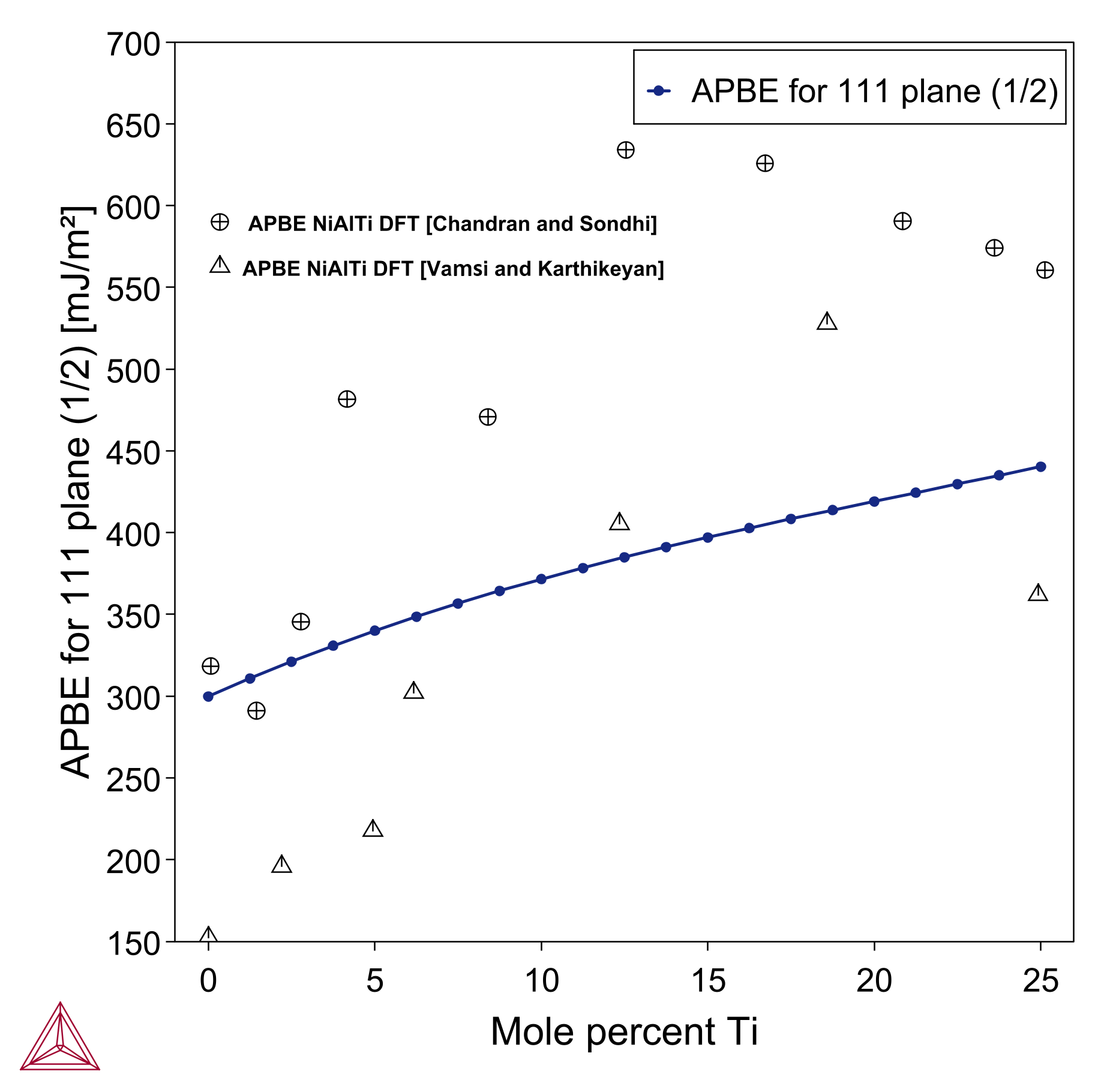
The Antiphase Boundary Energy Model calculates the antiphase boundary energy for Ni-base alloys with gamma prime (γ’) as the precipitate phase. The model is based on Miodownik et al. (1995), Saunders et al. (2000), Crudden et al. (2014), and Liu et al. (2018). See references.
The plot shows APBE surface energy for 111 plane as a function of composition of Ti (mole %) compared to experimental data from Vamsi et al. and Chandran et al. The calculation uses an Ni3Al1-xTix alloy at room temperature using a subset of phases for a typical Ni-base superalloy.
Coarsening Model
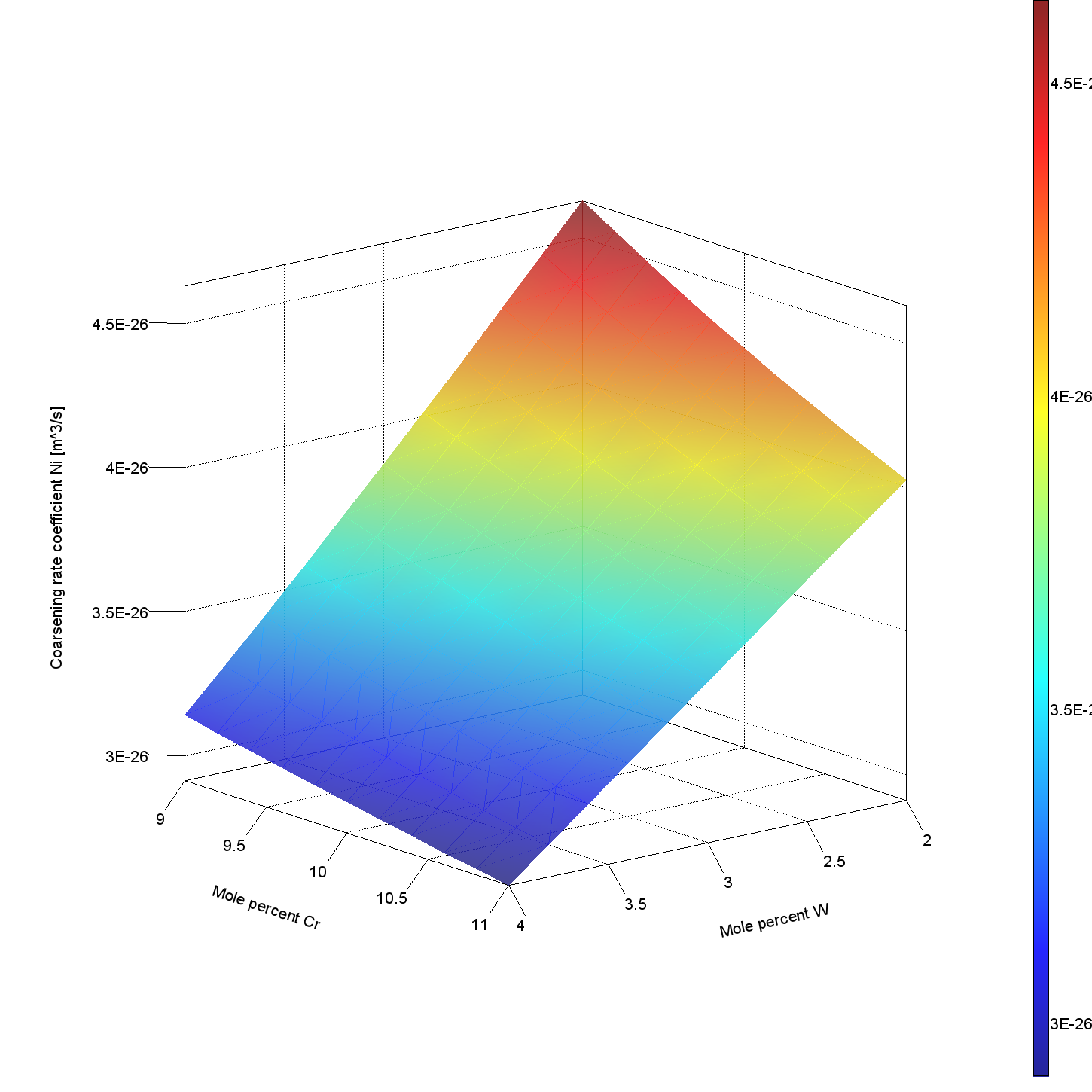
The Coarsening Model calculates the coarsening rate coefficient of one or several precipitate phases in a matrix phase, assuming spherical geometry of the precipitating phase(s). The model is based on Anderson et al. (1992) and Morral et al. (1994). See references.
The plot shows the calculated coarsening rate of γ’at 1000 °C for an Ni0.6Mo0.92Ta12.5Al1.83Ti10.5Cr3.3W alloy when changing the Cr and W content.
Equilibrium with Freeze-in Temperature Model
The Equilibrium with Freeze-in Temperature Model calculates equilibrium at the freeze-in temperature and evaluates the properties at a different temperature. The assumption is that diffusion and phase transformations are negligible when changing from the freeze-in-temperature and, therefore, that the phase amounts and compositions of phases are kept at all other temperatures.
The electrical resistivity due to phase interface scattering is evaluated as the scattering constant times sum of the interaction between the volume fraction of all the phases. The contribution to thermal conductivity is assumed to be related to that of electrical resistivity, following the Wiedemann-Franz law. See references.
The plot shows the lattice parameters for gamma and gamma prime plotted against experimental data from Nathal et al. It is a one axis calculation of a Ni0.6Mo0.92Ta12.5Al1.83Ti10.5Cr3.3W alloy evaluated with a range of 20 °C to 1000 °C using the Equilibrium with Freeze-in Temperature Nickel Property Model in Thermo-Calc. The freeze-in temperature is set to 1000 °C.

Solvus for Ordered Phase Model
The Solvus for Ordered Phase – Ni Property Model calculates the solvus of ordered phases such as FCC_L12, BCC_B2, NI3TA_D0A, NI3TI_D024, TCP-phases (Sigma), and so forth. The Model chooses the correct composition set by minimizing the Gibbs energy, which means that the composition set is identified automatically by the software for you.
The plot shows the solvus temperatures for NI3TA_D0A (Delta) and BCT_D022 (Gamma double-prime) compared to experimental data from Frank et al. It was calculated using the Solvus for Ordered Phase – Ni Property Model in Thermo-Calc.

Strain-Age Cracking Model
Welding or additive manufacturing (AM) of Ni-based alloys has so far been strongly limited by various cracking issues during processing or post-processing, such as strain-age cracking (SAC). The Strain-Age Cracking Property Model, developed by Kaplan, is applicable to welded or additively manufactured components, where there are interface strains between γ’ (gamma prime) and the matrix. The model can be performed in two modes, single temperature or temperature interval. In the former mode, the SAC risk is evaluated at a single temperature, and in the latter, the SAC risk is evaluated for an interval (default is from 1000 K up to gamma prime solvus). A negative or close to zero SAC risk factor value implies no or low risk for SAC. The risk for SAC increases as the risk factor value increases.
The plot shows a comparison of experimental alloys from Zhou et al. designed to have a large gamma prime fraction but a low risk for SAC, compared to CM247 LC, which is known to be very difficult to weld. This is reflected in a very high SAC risk factor for the latter.
![A parallel plot of the resulting SAC risk factor along with experimental and calculated solvus of γ’ for the three alloys compared in [2020Zho].](https://thermocalc.com/wp-content/uploads/Images/Plots/parallel-plot-of-resulting-sac-risk-factor-for-three-alloys.gif)
Nickel Model Library Examples
The Nickel Model Library includes three examples to help users get started. The examples are available from within the software from the Help menu > Example Files > Property models > Nickel.


